Lemme de Farkas-Minkowski
START
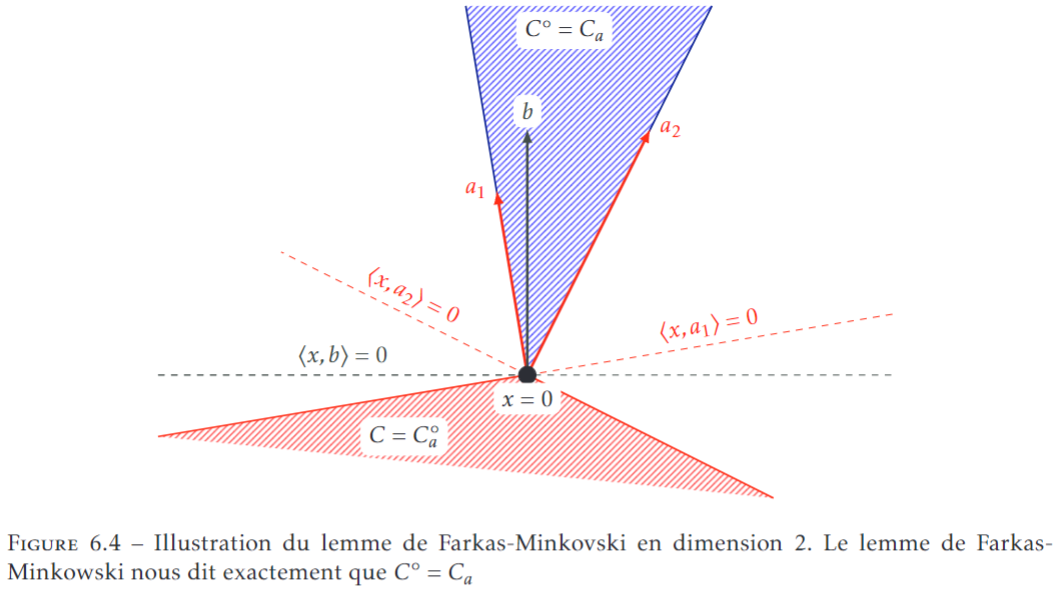
Théorème
Lemme de Farkas-Minkowski
Hypothèses:
- \(H\) est un Espace de Hilbert
- \((a_j)_{j\in J}\) est une famille finie de vecteurs de \(H\)
- \(C:=\{z\in H\mid\forall j\in J,\langle{z,a_i}\rangle _H\leqslant0\}\)
- \(b\in H\)
Résultats:
- on a l'équivalence :
- \(\forall x\in C,\langle{b,x}\rangle \leqslant0\), i.e. \(b\in C^\circ\)
\(\exists\mu\in{\Bbb R}^J_+\) tq \(b=\sum_{j\in J}\mu_ja_j\)
Equivalence?:
Résumé: Si un vecteur est dans le
Cône polaire d'un
Polaire d'une famille de vecteurs, alors il est engendré par cette famille.
END
